Adaptive Algorithm for Multi-Armed Bandit Problem with High-Dimensional Covariates (Inst. Statistics, Prof. Ching-Kang Ing)
Department: Institute of Statistics PI's Name: Ching-Kang Ing
Journal: Journal of the American Statistical Association
Title: Adaptive Algorithm for Multi-Armed Bandit Problem with High-Dimensional Covariates
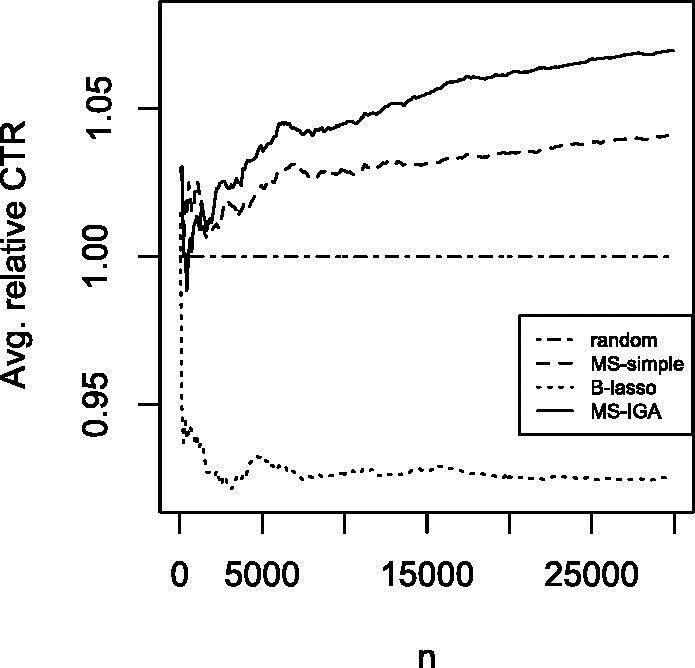
Abstract: This article studies an important sequential decision making problem known as the multi-armed stochastic bandit problem with covariates. Under a linear bandit framework with high-dimensional covariates, we propose a general multi-stage arm allocation algorithm that integrates both arm elimination and randomized assignment strategies. By employing a class of high-dimensional regression methods for coefficient estimation, the proposed algorithm is shown to have near optimal finite-time regret performance under a new study scope that requires neither a margin condition nor a reward gap condition for competitive arms. Based on the synergistically verified benefit of the margin, the algorithm exhibits adaptive performance that automatically adapts to the margin and gap conditions, and attains optimal regret rates simultaneously for both study scopes, without or with the margin, up to a logarithmic factor. Besides the desirable regret performance, the proposed algorithm simultaneously generates useful coefficient estimation output for competitive arms and is shown to achieve both estimation consistency and variable selection consistency. Promising empirical performance is demonstrated through extensive simulation and two real data evaluation examples.